FEM – Berechnung
Definition, Ablauf der Berechnung, Tipps und Hinweise
Definition FEM
Die Finite-Elemente-Methode, Abkürzung FEM (engl.: FEA – Finite Element Analysis) ist ein numerisches Verfahren zur Lösung physikalischer Probleme. Grundidee ist die Zerlegung (Diskretisierung) des Berechnungsgebietes in kleine, einfache Formen wie beispielsweise Dreiecke oder Rechtecke (2D-Elemente) sowie Tetraeder oder Quader (3D-Elemente) – den finiten Elementen. Durch dieses Vorgehen kann das Verhalten komplexer Geometrien auf der Elementebene formuliert werden. Das Verhalten der Gesamtstruktur ergibt sich dann aus der Kombination des Einzelelementverhaltens. Dieses Vorgehen hat den Vorteil, dass physikalische Aufgabenstellungen für komplexe Strukturen gelöst werden können, für die keine analytische Lösung existiert oder bekannt ist.
Eine große Verbreitung hat die FEM in der Festigkeitsbewertung – beispielsweise im Maschinenbau und Bauingenieurswesen – erlangt.
FEM-Berechnung – Der Ablauf
Der Ablauf einer FE-Berechnung erfolgt in drei Schritten: dem Preprocessing (1), dem Lösen des Gleichungssystems mit dem Solver (2) und dem Postprocessing (3). Diese drei Schritte werden in folgenden Abschnitten näher erläutert und in einem Video visuell dargestellt.
Ablauf einer FEM-Berechnung im Zeitraffer
Das Video zeigt die Analyse einer Schraubenverbindung Rotorwelle-Rotornabe einer Windkraftanlage. Es werden folgende Schritte gezeigt:
- Einlesen der 3D-CAD-Geometrie des Konstrukteurs
- Aufbereitung der Geometrie
- Vernetzung
- Definition der Randbedingungen
- Lösung des nichtlinearen Differentialgleichungssystems mit Hilfe von Ansys
Ergebnisauswertung
(1) Preprocessing
Ziel des Preprocessing ist die Vorbereitung eines rechenfähigen Finite-Elemente-Modells für den Solver, also die Unterteilung der Struktur in finite Elemente sowie die Definition von Randbedingungen, Materialen und Kontakten. Dies geschieht in folgenden Schritten.
Blog-Artikel zum Preprocessing
Geometriebereitstellung
Oftmals liegt die Geometrie bereits in einem CAD-Format vor. Dieses wird im FE-Programm importiert. Alternativ kann die Geometrie auch im FE-Programm erzeugt werden.
Da nicht notwendigerweise alle Geometriedetails benötigt werden, erfolgt meist eine Vereinfachung der Geometrie. Dies beinhaltet löschen von nicht benötigten Körpern, unterdrücken von unwesentlichen Geometriedetails wie z.B. Fasen, irrelevante Bohrungen und kleinen Radien. Außerdem werden gegebenenfalls 3D-Geometrien in 1D-Geometrien (Balken) bzw. 2D-Geometrien (Schalen) umgewandelt. Diese Änderungen werden durchgeführt, um die Anzahl der Knoten und damit den Berechnungsaufwand zu reduzieren.
Um den nachfolgenden Vernetzungsprozess zu erleichtern, der heutzutage meist automatisch erfolgt, werden komplexe Bauteile oft in einfachere Geometrien zerschnitten.
Vernetzung
Durch die Vernetzung wird der Körper in finite Elemente unterteilt. Typischerweise werden durch das FE-Programm folgende Elemente bereitgestellt:
- Eindimensionale Elemente
- Stäbe
- Balken
- Zweidimensionale Elemente (als Dreieck- und Viereck-Elemente)
- Membrane
- Platten
- Schalen
- Dreidimensionale Elemente
- Tetraeder
- Hexaeder
Die Elemente unterscheiden sich auch in den Ansatzfunktionen und beinhalten deswegen zum Teil auch Mittelknoten.
Die Vernetzung erfolgt heutzutage meist automatisch, so dass durch den Berechnungsingenieur nur eine Vorgabe über den Elementtyp und die Elementgröße erfolgen muss. Für die automatische Vernetzung werden meist Tetraederelemente verwendet, da eine Vernetzung mit Hexaedern nur für sehr einfache Geometrien automatisch gelingt.
Randbedingungen
Für die Erstellung des Modells müssen auch Randbedingungen definiert werden. Dafür müssen die Lasten auf dem Modell definiert werden, wie beispielsweise:
- Kräfte
- Drücke
- Beschleunigungen
Außerdem muss die Lagerung des Modells sichergestellt werden.
Materialdefinition
Im Preprozessor werden auch die Materialien definiert und den entsprechenden Körpern bzw. Elementen zugewiesen.
Kontakte
Unterschiedliche Körper können über gemeinsame Knoten miteinander verbunden werden. Diese Verbindungen sind nur möglich, wenn die beiden Körper an der Schnittstelle ein gleiches Netz aufweisen. Durch die Verschmelzung der Knoten ergibt sich dann eine feste Verbindung.
Falls keine koinzidenten Knoten vorliegen oder eine nichtlineare Interaktion zwischen den Körpern gewünscht ist (Beispiel: reibbehafteter Kontakt), so müssen zwischen den Körpern Kontakte gesetzt werden.
(2) Solver
Der Solver erzeugt aus den übergebenen Element- und Materialdefinitionen Steifigkeitsmatrizen sowie je nach Problem auch Masse- und Dämpfungsmatrizen. Die Steifigkeitsmatrizen der einzelnen Elemente werden dann in einer Gesamtsteifigkeitsmatrix K assembliert. Mit dem Vektor der Knotenverschiebung d und dem Kraftvektor f ergibt sich dann folgendes Gleichungssystem für den statischen Fall (Masse- und Dämpfungsmatrix sind nicht relevant und fehlen daher):
K d = f
Der Vektor d enthält für jeden Knoten eines Volumenelements die 3 Verschiebungskomponenten x, y und z. Für Schalen und Platten sowie Balken kommen noch bis zu 3 Verdrehungen hinzu, so dass pro Knoten bis zu 6 Freiheitsgrade existieren. Für ein Volumenmodell mit 500 000 Knoten (typische Größe im Berechnungsalltag) ergeben sich somit 1.5 Millionen Freiheitsgrade.
Dieses Gleichungssystem wird nun vom Solver gelöst. Liegt ein nichtlineares Problem vor – beispielsweise durch abhebende Kontakte, große Verformungen oder plastisches Materialverhalten – so hängt die Steifigkeitsmatrix vom Verschiebungsvektor d ab. Für diesen Fall muss das Gleichungssystem mehrmals iterativ unter Anpassung der Steifigkeitsmatrix gelöst werden, was zu sehr hohen Rechenzeiten führen kann.
Nach der Lösung des Gleichungssystems berechnet der Solver unter Verwendung des Verschiebungsvektors d die Spannungen und Dehnungen im Element sowie die Knotenkräfte.
Blog-Artikel zum Solver
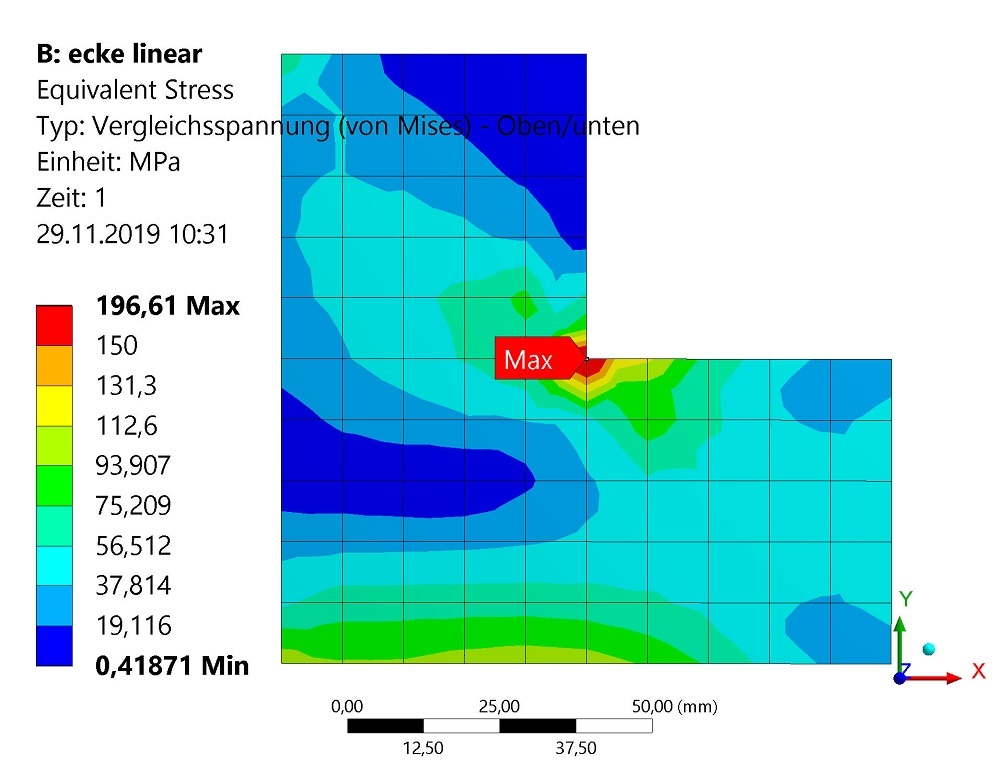
(3) Postprocessing
Im Postprocessing erfolgt die Auswertung der Ergebnisse der FE-Berechnung. Aufgrund der Vielzahl an Ergebnissen, die durch die meist hohe Elementanzahl verursacht wird, ist die graphische Darstellung der Ergebnisgrößen weitverbreitet. Dafür werden Farbplots verwendet, die es ermöglichen, einen schnellen Überblick über die Ergebnisse zu bekommen.
Auf diese Art können alle Ergebnisse dargestellt werden, die während der Lösung des Gleichungssystems erzeugt wurden. Außerdem werden im Postprocessing oft noch zusätzliche Ergebnisse erzeugt. Ein Beispiel sind Vergleichsspannungen, die ausgehend vom vorliegenden Spannungstensor berechnet werden.
Die Verformung wird oft über die Anzeige der verformten Struktur dargestellt. Eine Überhöhung der Verformungen wird genutzt, um die üblicherweise kleinen, realen Verformungen sichtbar zu machen.
Das Postprocessing beinhaltet auch den Export der Daten. Eine Weiterverarbeitung für Nachweise der Betriebsfestigkeit, von Schweißnähten und Schrauben u.a. kann dann in Excel, Matlab oder anderen Programmen erfolgen.
Blog-Artikel zum Postprocessing
Artikel veröffentlicht am 02.12.2019
Andreas Hanke
Dipl.-Ing. Maschinenbau
Autor | ✉ ahanke@ing-hanke.de
Sie haben Anmerkungen, Ideen oder Fragen: Schreiben Sie mir an ahanke@ing-hanke.de oder rufen Sie mich an (0381/121 579 10).
Diese Artikel könnten Sie auch interessieren
Dienstleister für
FEM-Simulation
Dienstleistungen für FEM-Berechnung vom Spezialisten finden Sie hier…