Einleitung
Bei der linearen Berechnung von Bauteilen mit Hilfe der Finite-Elemente-Methode (FEM) kommt es an lokalen Kerben oft zu sehr hohen Spannungen, die die Streckgrenze überschreiten. In diesem Artikel betrachten wir, wie viele dieser Bauteile trotzdem mit einer plastischen Rechnung nachgewiesen werden können. Außerdem wird gezeigt, wie groß die Reserven bei scharfen Kerben sein können.
Die Spannungsüberhöhungen an gekerbten Bauteilen sind nicht durch Singularitäten verursacht (Artikel zum Erkennen und zum Umgang mit Singularitäten) und konvergieren im Zuge der Netzverfeinerung. Ursache sind Querschnittsveränderungen und Kerben, an denen der Kraftfluss zwischen Einspannung und Krafteinleitung gestört wird.
Viele Werkstoffe weisen materielle Nichtlinearitäten auf, welche durch das Vorhandensein einer Streckgrenze charakterisiert sind. Das heißt, dass sich nach Erreichen der Streckgrenze der lineare Verlauf des Spannungs-Dehnungs-Diagramms, „Hookesche Gerade“ genannt, abrupt ändert und das Material durch spezielle Umlagerungsprozesse zu „fließen“ beginnt, also plastifiziert. Aus diesem Grund wird die Streckgrenze auch Fließgrenze (engl. yield strength) genannt.
Bei ungekerbten Bauteilen kommt es nach dem Einsetzen von Verfestigungsmechanismen zu einer Plastifizierung des gesamten Querschnittes (vollplastischer Zustand). Nachdem die Plastifizierungsreserven erschöpft sind und die plastische Dehnung des Materials den kritischen Wert der Bruchdehnung erreicht kommt es zum Bruch des Bauteils.
Bei gekerbten Bauteilen führen die Spannungsüberhöhungen zunächst nur lokal zu Umlagerungen im Material und erst im Anschluss daran zum Durchplastifizieren des Querschnittes. Je schärfer dabei die Kerbe ist, umso größer ist der Effekt der Spannungsumlagerung. Die umliegenden Bereiche übernehmen einen Teil der Beanspruchungen und bilden somit die Grundlage für die plastische Reserve eines Bauteils.
In dieser Untersuchung werden zwei Bauteile mit gleicher Geometrie, jedoch unterschiedlichen Werkstoffeigenschaften (Baustahl S355 und Eisenguss GJL-300) betrachtet. Der Baustahl hat eine vergleichsweise hohe Duktilität, während der Grauguss sehr spröde ist. Das Vorgehen orientiert sich an der FKM-Richtlinie „Rechnerischer Festigkeitsnachweis für Maschinenbauteile aus Stahl- Eisenguss- und Aluminiumwerkstoffen“ von 2012.
Modellbeschreibung
Die Geometrie des Bauteiles ist in der folgenden Abbildung dargestellt. Es handelt sich um einen gekerbten Blechstreifen (50 mm · 150 mm) der Dicke t = 5 mm. Die Kerbe mit Halbkreiskontur ist so modelliert, dass die Restbreite des Bleches an der Kerbstelle der Hälfte der ursprünglichen Breite entspricht.
Krafteinleitung und Lagerung erfolgen an den beiden kurzen Seiten. Die angetragene Kraft beträgt 20000 N beim Stahlblech und 8000 N beim Graugussteil für die lineare Rechnung.
Die Berechnungen werden für beide Materialien sowohl mit ausschließlich linearem Materialverhalten, als auch mit bilinearem Materialverhalten (Abknickpunkt bei Rp, ideal plastisch) durchgeführt.
Die Materialdaten sind in der folgenden Tabelle zusammengefasst.
| Parameter | Einheit | Wert | |
| S355 | GJL-300 | ||
| Streckgrenze | MPa | 355 | 195 |
| Zugfestigkeit | MPa | 470 | 300 |
| Elastizitätsmodul | MPa | 210000 | 100000 |
| Querkontraktion | – | 0.3 | 0.25 |
Für die S355-Probe ergibt sich folgendes Spannungs-Dehnungs-Diagramm:
Ergebnisse
FE-Berechung
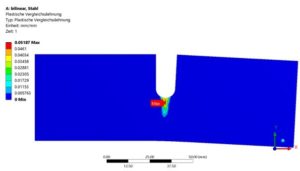
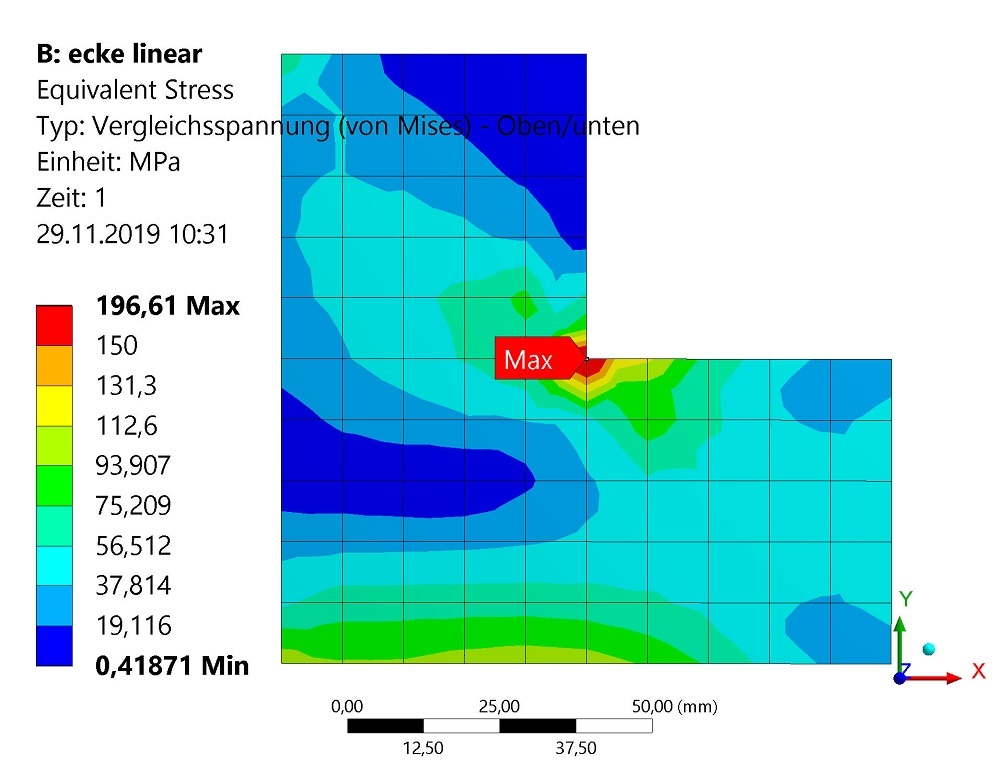
Die Spannungen (von Mises) und die plastischen Dehnungen sind auf den folgenden Abbildungen beispielhaft für den Stahlblechstreifen dargestellt.
von-Mises-Vergleichsspannung am gekerbten Bauteil – lineares Materialverhalten
von-Mises-Vergleichsspannung am gekerbten Bauteil – bilineares Materialverhalten
plastische Vergleichsdehnungen am gekerbten Bauteil – bilineares Materialverhalten
In der folgenden Tabelle sind die Ergebnisse der FEM-Berechnungen zusammengefasst.
| Parameter | Materialverhalten | Einheit | Wert | |
| S355 | GJL-300 | |||
| Max. von-Mises- Vergleichsspannungen | Linear | MPa | 1242 | 497 |
| Max. von-Mises- Vergleichsspannungen | Bilinear | MPa | 355 | 195 |
| Max. plastische Dehnung | Bilinear | – | 5.2 % | 0.9 % |
Nachweise
Die folgenden Nachweise orientieren sich an der FKM-Richtlinie. Um eine einfache Nachvollziehbarkeit zu gewährleisten, wurde auf die Berücksichtigung von Sicherheitsfaktoren verzichtet. Die Nachweise sind vom Grad der Konservativität absteigend bzw. vom Berechnungsaufwand (abgesehen vom Nennspannungsnachweis) aufsteigend sortiert:
- Nachweis der örtlichen elastischen Spannungen gegen die Streckgrenze („klassischer“ Nachweis gegen die Streckgrenze). Die Grenztragfähigkeit wird über die lineare Skalierung „zulässige Spannung/maximale Spannung im FE-Modell x Kraft“ berechnet
- Nachweis der plastischen Dehnungen gegen die minimale ertragbare Dehnung bei hoher Mehrachsigkeit ε0 (Nachweis gegen lokalen Anriss in der Kerbe). Die Grenztragfähigkeit wird durch schrittweise Erhöhung der Kraft im FE-Modell bis zum Auftreten der zulässigen Dehnung ermittelt.
- Nachweis der plastischen Dehnungen gegen die ertragbare Dehnung εertr unter Berücksichtigung der real auftretenden Mehrachsigkeit (Nachweis gegen lokalen Anriss in der Kerbe). Die Grenztragfähigkeit wird durch schrittweise Erhöhung der Kraft im FE-Modell bis zum Auftreten der zulässigen Dehnung ermittelt.
- Nachweis gegen plastischen Kollaps (Nachweis gegen Grenztragfähigkeit im durchplastifizierten Zustand). Zur Ermittlung des Grenzzustandes plastischer Kollaps wird die Kraft schrittweise erhöht, bis in der FE-Simulation keine Konvergenz mehr erzielt wird.
Für den plastischen Nachweis ist das Minimum der Lasterhöhung aus den Nachweisen 3 und 4 zu berechnen. Damit wird berücksichtigt, ob der lokale Anriss oder die plastische Grenztragfähigkeit für die jeweilige Struktur limitierend ist.
Die in den folgenden Tabellen dargestellten Grenzlasterhöhungen geben den Faktor der ertragbaren Kraft im jeweiligen Grenzzustand im Vergleich zur ertragbaren Kraft für Nachweis 1 (örtliche elastische Spannungen gegen Streckgrenze) an.
| Nachweis | Nachweisgrenze | Grenzlast in N | Grenzlasterhöhung |
| Lokale lineare Spannungen gg. Streckgrenze | Rp 0,2 = 355 MPa | 5718 | 1.00 |
| Ertragbare Dehnung ε0 (FKM) | ε0 = 5.0 % | 19961 | 3.49 |
| Ertragbare Dehnung εertr (FKM) | εertr = 10.3 % | 20382 | 3.56 |
| Vollplastische Grenztragfähigkeit (FKM) | Konvergenz des FE-Modells | 20641 | 3.61 |
| Nachweis | Nachweisgrenze | Grenzlast in N | Grenzlasterhöhung |
| Lokale lineare Spannungen gg. Streckgrenze | Rp 0,1 = 195 MPa | 3141 | 1.00 |
| Ertragbare Dehnung ε0 (FKM) | ε0 = 0.195 % | 3141.2 | 1.00 |
| Ertragbare Dehnung εertr (FKM) | εertr = 0.199 % | 3206 | 1.02 |
| Vollplastische Grenztragfähigkeit (FKM) | Konvergenz des FE-Modells | 11340 | 3.61 |
Fazit
Es ist deutlich zu erkennen, dass der duktile S355 für die vorliegende scharfe Kerbe eine sehr große Nachweisreserve gegenüber einer elastischen Rechnung bietet: mit einer plastischen Rechnung erhöht sich die nachweisbare Tragfähigkeit um den Faktor 3.6. Aufgrund der hohen Duktilität des Werkstoffes liegt der Grenzzustand „lokaler Anriss“ und „plastischer Kollaps“ sehr nahe beieinander.
Bei dem sehr spröden GJL-300 erfolgt der lokale Anriss schon bei einer Erhöhung der Kraft von 2% gegenüber der elastischen Rechnung. Durch eine plastische Rechnung ist somit kaum ein Potential zu erschließen. Der plastische Kollaps erfolgt durch den frühen Anriss bei der Graugussgeometrie bei wesentlich höheren Lasten.
Artikel veröffentlicht am 21.01.2020
Martin Lork
Dipl.-Ing. Maschinenbau
Autor | ✉ mlork@ing-hanke.de
Andreas Hanke
Dipl.-Ing. Maschinenbau
Co-Autor | ✉ ahanke@ing-hanke.de
Sie haben Anmerkungen, Ideen oder Fragen: Schreiben Sie mir an mlork@ing-hanke.de oder rufen Sie mich an (0381/121 579 12).
Diese Artikel könnten Sie auch interessieren
Dienstleister für
FEM-Simulation
Dienstleistungen für FEM-Berechnung vom Spezialisten finden Sie hier…