Was genau sind Singularitäten in der FEM, wo treten sie auf und was ist bei der Bewertung zu beachten?
Jedem FE-Berechnungsingenieur läuft früher oder später eine Singularität über den Weg. Die „Lösung“ für dieses Problem ist relativ vielfältig und reicht von einem lapidaren „das ist eine Singularität, das kann man ignorieren“ bis zu „die Spannungen sind viel zu hoch, das hält nicht“.
Beim Bearbeiten von Kundenprojekten haben wir regelmäßig mit Singularitäten zu tun (z.B. bei Schweißnahtberechnungen, oder bei Nachweisen von Schraubenverbindungen, etc. – hier geht es zu unserem vollständigen Leistungsangebot FEM-Berechnung). Dementsprechend haben wir einiges an Erfahrung und Wissen in diesem Zusammenhang vorzuweisen, welches wir an dieser Stelle mit Ihnen teilen möchten.
Für einen sichereren Umgang mit Singularitäten, erörtert dieser Artikel die folgende Punkte:
- Was ist eine Singularität eigentlich?
- Welche Arten von Singularitäten gibt es?
- Wie gehe ich mit Singularitäten um?
Was ist eine Singularität eigentlich?
Hinweis: Eine Singularität im Sinne einer singulären Steifigkeitsmatrix, verursacht durch eine ungenügende Anzahl an Randbedingungen, ist nicht Inhalt dieses Artikels.
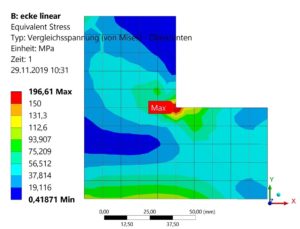
Als Singularitäten bezeichnet man im FE-Modell Stellen, an denen eine Netzverfeinerung zu immer weiter steigenden Spannungen, Dehnungen oder Verformungen führt (hier auf die Strukturmechanik bezogen; die anderen Berechnungsdisziplinen wie z.B. Elektrostatik, Wärmeleitung u.s.w. werden hier nicht behandelt). D.h. die Spannungen konvergieren nicht zu einem Endwert, sondern steigen bei unendlich feinem Netz unendlich hoch an. Ein Beispiel ist der abgebildete Winkel.
Mit zunehmender Netzfeinheit zeigen sich an der einspringenden Ecke immer höhere Spannungen. Der Spannungsgradient im Bereich der Spannungsspitzen ist sehr hoch. Die maximale Spannung in Abhängigkeit von der Netzfeinheit sieht man in folgendem Diagramm:
Es wird häufig argumentiert, dass es in der Realität keine unendlich hohen Spannungen gibt. Rechnet man das obige Beispiel mit einem nichtlinearen Materialverhalten, so ergeben sich logischerweise keine unendlichen Spannungen mehr. Stattdessen werden die Dehnungen unendlich hoch, so dass ein Nachweis immer noch nicht geführt werden kann.
Ein weiteres Argument ist, dass der Radius in Realität nie unendlich scharf sein kann. Unter Annahme eines realen Radius lässt sich für das gegebene Beispiel zwar ein Nachweis führen. Die Bewertung ist allerdings schwierig, da zulässige Dehnungen für extrem scharfe Kerben in den üblichen Berechnungsrichtlinien (z.B. FKM-Richtlinie) nicht angegeben werden.
Welche Arten von Singularitäten gibt es?
Für Singularitäten gibt es unterschiedliche Ursachen:
Einspringende Ecken
Einspringende Ecken wie das obige Beispiel sind das Paradebeispiel für eine Singularität. Zu beachten ist, dass der Winkel nicht unbedingt 90 ° betragen muss. Singularitäten treten bereits bei Winkeln kleiner als 180° auf.
Unterschiedliche Möglichkeiten, um mit dieser Art von Singularitäten umzugehen, finden sich weiter unten.
Lasteinleitung
Diese Singularitäten sind immer durch die Vereinfachung der Modellierung verursacht, da es Punkt- und Linienlasten sowie unendlich steife Einspannungen in der Realität nicht gibt. Wenn klar ist, dass diese Stellen nicht kritisch sind, da sie beispielsweise außerhalb des Bereiches liegen, der ausgewertet werden soll, können sie getrost ignoriert werden.
Sofern nicht klar ist, ob die dementsprechenden Bereiche kritisch sind, so ist die Modellierung realistischer zu gestalten. Welche Kombinationen von Lasten und Elementtypen sich nicht singulär verhalten ist hier zu finden.
Randbedingungen
An Einspannungen können ebenfalls Singularitäten auftreten. Die Vorgehensweise erfolgt entsprechend dem Vorgehen bei Singularitäten durch Lasteinleitungen: Wenn man an der jeweiligen Stelle auswerten will, muss man genauer modellieren. Wenn nicht, kann man die Singularität ignorieren.
Kontakte
Im Kontaktbereich zwischen zwei unterschiedlichen Bauteilen treten ebenfalls häufig Singularitäten auf. Häufig werden durch Kontakte Singularitäten verursacht, weil die zwei aneinander angrenzenden Körper bei einer „Verschmelzung“ eine einspringende Ecke bilden. Dementsprechend können diese Singularitäten oft wie Ecksingularitäten behandelt werden.
Eine Besonderheit stellen reibbehaftete Verbindungen dar, wie sie beispielsweise bei Pressverbindungen vorliegen. Der Schädigungsmechanismus durch Reibkorrosion und die damit verbundenen Rissinitiierung unter dynamischen Lasten lässt sich mit der Finite-Elemente-Methode nicht darstellen. Diese Stellen können vorteilhaft mit Nennspannungen unter Verwendung geeigneter Kerbwirkungszahlen bewertet werden.
Verbindungen zwischen unterschiedlichen Elementtypen
Am Übergang von einem auf einen anderen Elementtyp (beispielsweise von Volumen- auf Schalenelemente) können ebenfalls Singularitäten auftreten. Übergänge in Modellbereichen, die ausgewertet werden sollen, sollten daher vermieden werden.
Verbund unterschiedlicher Materialien
Auch beim Verbund unterschiedlicher Materialen kann eine Singularität auftreten. Ein Beispiel ist ein Stahleinleger in einer GFK-Struktur mit einem scharfen Übergang. Eine Bewertung kann über die Bruchmechanik erfolgen. Eine andere Lösung ist – wenn angemessen – das Vermeiden scharfer Übergänge.
Wie gehe ich mit Singularitäten um?
Sofern in einem FE-Modell eine Singularität auftritt, stellt sich natürlich sofort die Frage, wie sich diese in der Realität auswirkt. Für das Beispiel der oben gezeigten einspringenden Ecke zeigen sich in der Realität folgende Unterschiede:
- Eine ideal scharfe Kante tritt in der Realität nicht auf, sondern eher eine Verrundung mit einem sehr kleinen Radius
- Das Material ist nur makroskopisch betrachtet homogen. Bei einer mikroskopischen Betrachtung, die die Körner des Materials mit einbezieht, ist nicht die mechanische Spannung, sondern die „Kraft pro Korn“ für das Versagen wesentlich. Diese Kraft zeigt kein singuläres Verhalten. Es ergibt sich folgendes Bild an der einspringenden Ecke.
 Auf die Körner wirken nun keine Spannungen mehr, sondern Kräfte. Das Integral der Spannung über die Fläche (die auf das Korn wirkende Kraft) ist nicht singulär, auch bei einer unendlich hohen Spannung an der Ecke.
Auf die Körner wirken nun keine Spannungen mehr, sondern Kräfte. Das Integral der Spannung über die Fläche (die auf das Korn wirkende Kraft) ist nicht singulär, auch bei einer unendlich hohen Spannung an der Ecke.
Diese Unterschiede zwischen FE-Modell und Realität führen dazu, dass Bauteile in der Realität halten, deren Spannungen im FE-Modell die Streck- oder auch Bruchgrenze des Materials überschreiten. Allerdings sind singuläre Stellen im FE-Modell auch meist in der Realität kritische Stellen. Daher ist es notwendig, diese Stellen mit alternativen Methoden zu beurteilen. Mögliche Herangehensweisen finden sich unten.
Sofern die Singularität in einem Bereich des Modells auftritt, der nicht ausgewertet werden soll, so können die Singularitäten natürlich im Modell belassen werden.
Ecksingularitäten unter Extremlast
Für die Bewertung von Singularitäten unter Wirkung einer Extremlast bieten sich folgende Möglichkeiten an:
Bewertung mit kleinem Radius
Der kritische Bereich wird mit einem kleinen Radius verrundet, der üblicherweise der realen Geometrie entspricht oder eine konservative Abschätzung des kleinsten auftretenden Radius darstellt. Ein Radius von beispielsweise 0.1 mm wird bei einer spanenden Fertigung sicherlich nur in seltenen Fällen unterschritten. Dann folgt eine Bewertung dieser Stelle. Ein nichtlineares Materialgesetz kann natürlich verwendet werden.
Eine auf diese Art durchgeführte Bewertung ist konservativ. Insbesondere ist zu bedenken, dass die berechneten lokalen, plastischen Dehnungen nur sehr kleinräumig auftreten. Ein Vergleich mit den durch beispielsweise die FKM-Richtlinie vorgegebenen zulässigen Dehnungen, die sich eher an den global ermittelten Dehnungen einer Zugprobe orientieren, sind als konservativ anzusehen.
Bewertung mit der Bruchmechanik
 Eine Bewertung kann auch mit der Bruchmechanik erfolgen. Zu diesem Zweck wird an der einspringenden Ecke ein möglicher Riss modelliert und mit Hilfe von bruchmechanischen Methoden bewertet. Der Aufwand für solch ein Vorgehen ist relativ hoch und kann nur in Ausnahmefällen empfohlen werden.
Eine Bewertung kann auch mit der Bruchmechanik erfolgen. Zu diesem Zweck wird an der einspringenden Ecke ein möglicher Riss modelliert und mit Hilfe von bruchmechanischen Methoden bewertet. Der Aufwand für solch ein Vorgehen ist relativ hoch und kann nur in Ausnahmefällen empfohlen werden.
Bewertung anhand von Nennspannungen
Sofern ein ausreichendes Plastifizierungsvermögen gegeben ist, kann auch eine Bewertung anhand von Nennspannungen erfolgen. Dies ist typischerweise für Schweißnähte der Fall. Es ist allerdings darauf zu achten, dass die Nennspannung über einen nicht zu großen Bereich gebildet wird: damit wird vermieden, dass die Naht schon vor Überschreiten der zulässigen Nennspannung durch übermäßiges Plastifizieren versagt. Vage Hinweise für die Schweißnahtlänge, über die gemittelt werden darf, finden sich beispielsweise im Eurocode 3.
Ecksingularitäten unter dynamischer Last
Bewertung anhand von Kerbwirkungszahlen
Für manche Geometrien liegen experimentell ermittelte Kerbwirkungszahlen vor. In diesem Fall ist es sinnvoll, die Bewertung anhand außerhalb der Singularität ermittelter Spannungen vorzunehmen und die Wirkung der Singularität durch die dementsprechenden Kerbwirkungszahlen vorzunehmen.
Bewertung von Schweißnähten
Schweißnähte können mittels des Nennspannungskonzeptes bzw. des Strukturspannungskonzeptes, beispielsweise gemäß Eurocode 3, bewertet werden. Eine weitere Möglichkeit der Bewertung – insbesondere für sehr komplexe Nahtgeometrien und Wurzelrisse – stellt die Verwendung des Kerbspannungskonzeptes dar. Allen Verfahren ist gemein, dass die Singularität nicht mit ausgewertet wird: die schwingfestigkeitsmindernde Wirkung der scharfen Kerbe wird auf Seite der ertragbaren Spannungen berücksichtigt.
Bewertung mittels Ersatzradien
Die Stützwirkung im Material, die dazu führt, dass im Kerbgrund höhere Spannungen als in ungekerbten Bauteilen ertragen werden können, kann auch durch die Einführung eines Ersatzradius berücksichtigt werden. Die Höhe der fiktiven Radiusvergrößerung ergibt sich aus der Ersatzstrukturlänge des Materials (beispielsweise in der FKM-Richtlinie enthalten) und einem Faktor s, der vom Beanspruchungsfall abhängt. Diese Methode geht auf Neuber und Radaj zurück.
Bewertung mittels der Bruchmechanik
Wie bei statischen Lasten, so ist natürlich auch unter dynamischer Last die Bewertung mittels der Bruchmechanik möglich. Anhand der Spannungsintensitätsfaktoren kann eine Rissfortschrittsberechnung erfolgen, die das Wachstum eines angenommenen Risses beschreibt. Dieses Verfahren sollte man aufgrund des Aufwandes nur verwenden, wenn keine alternativen Berechnungsmethoden zur Verfügung stehen.
Durch Lasteinleitung verursachte Singularitäten
Eine Singularität kann durch die Art der Lasteinleitung verursacht werden. Ob Singularitäten der Verformungen oder Spannungen auftreten, kann den folgenden Tabellen entnommen werden. Diese Arten von Singularitäten sind einfach zu behandeln. Wenn diese Stellen in Modellbereichen liegen, die ausgewertet werden sollen, so ist die Art der Lasteinleitung realistischer zu gestalten. Wenn nicht, dann spricht nichts dagegen, diese Singularitäten so im Modell zu belassen.
Verursacht die Lasteinleitung eine Singularität bezüglich der Verformungen?
| Balkenelement | Schalenelement | Volumenelement | |
| Punktlast | Nein | Nein | Ja |
| Linienlast | Nein | Nein | Nein |
| Flächenlast | – | Nein | Nein |
Verursacht die Lasteinleitung eine Singularität bezüglich der Spannungen?
| Balkenelement | Schalenelement | Volumenelement | |
| Punktlast | Nein | Ja | Ja |
| Linienlast | Nein | Nein | Ja |
| Flächenlast | – | Nein | Nein |
Artikel veröffentlicht am 29.11.2019


Martin Lork
Dipl.-Ing. Maschinenbau
Autor | ✉ mlork@ing-hanke.de
Andreas Hanke
Dipl.-Ing. Maschinenbau
Co-Autor | ✉ ahanke@ing-hanke.de
Sie haben Anmerkungen, Ideen oder Fragen: Schreiben Sie mir an mlork@ing-hanke.de oder rufen Sie mich an (0381/121 579 12).
Diese Artikel könnten Sie auch interessieren
Dienstleister für
FEM-Simulation
Dienstleistungen für FEM-Berechnung vom Spezialisten finden Sie hier…